我最近的project是关于LDPC的,所以读了一些关于LDPC的资料,只敢说略有了解。想想当初对LDPC的一片茫然,只想通过这几篇blog对一些需要帮助的朋友提供一些帮助。其实网上的LDPC的介绍,tutorial,多如牛毛,但是多是关于介绍LDPC的历史,decoding算法的描述。往往读完了之后一片茫然,也许这个算法是很棒,能够很好的进行decoding,但是这个算法是如何设计的,以及面对有特殊要求的code的时候,如何设计我们自己的LDPC,并没有一个很好的阐述,甚至不明白为什么算法会设计成这个样子。
我想通过这几篇blog来说明我对LDPC的认知,希望对大家有所帮助。这里强力推荐《modern coding theory》 by Tom Richardson and Rüdiger Urbanke,大师级的著作。的确很难读懂,但是这本书对coding的阐述非常系统,强烈建议读一下。
这篇post,我想先介绍一下LDPC最简单的问题,decoding algorithm。(如果你连什么是linear code,为什么有variable nodes和check nodes也不知道,请先wikipedia一下基础知识)
1.Message-Passing Rules
1.1 函数分解(factorizations)
学过概率的都知道如何求边缘分布(marginal distribution), , 对于任何函数来说,求marginal都是一样的方法。
, 对于任何函数来说,求marginal都是一样的方法。
例如,有一个函数
我们想求对于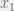 的marginal function,我们可以得到
的marginal function,我们可以得到
 ,
,
其中, 表示除
表示除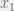 之外所有变量(variables)的和。
之外所有变量(variables)的和。
这里有一个很有意思的现象,假设每个变量的都有X个取值。 那么如果直接计算出 的
的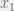 的所有取值需要
的所有取值需要 次计算。但是我们可以减少计算量,通过
次计算。但是我们可以减少计算量,通过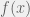 的分解形式。
的分解形式。
![f(x_1)=[\sum_{x_2,x_3}f_1(x_1,x_2,x_3)][\sum_{x_4}f_3(x_4)(\sum_{x_6}f_2(x_1,x_4,x_6))(\sum_{x_5}f_4(x_4,x_5))]](https://s0.wp.com/latex.php?latex=f%28x_1%29%3D%5B%5Csum_%7Bx_2%2Cx_3%7Df_1%28x_1%2Cx_2%2Cx_3%29%5D%5B%5Csum_%7Bx_4%7Df_3%28x_4%29%28%5Csum_%7Bx_6%7Df_2%28x_1%2Cx_4%2Cx_6%29%29%28%5Csum_%7Bx_5%7Df_4%28x_4%2Cx_5%29%29%5D&bg=f0f0f0&fg=555555&s=0&c=20201002)
第一个因式需要 次计算,第二个因式需要
次计算,第二个因式需要 次计算,相乘之后计算量还是
次计算,相乘之后计算量还是 , 因为
, 因为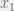 还有X个值,所以总共的计算量
还有X个值,所以总共的计算量 。 相比较前一个方法的计算量,这个方法把复杂度大大降低了。
。 相比较前一个方法的计算量,这个方法把复杂度大大降低了。
我们可以用树形图来表示刚才的例子。

其中,圆圈代表variable nodes,方块代表factor nodes。variable node总是与factor node相连接的。注意这里没有循环(cycle),也就是说,连接两个nodes只有一条边(edge)。
1.2 Recursive Determination of marginals
下面我们来讨论如何计算marginal。
如果我们想计算 ,并且g可以分解成树形图,那么我们可以计算
,并且g可以分解成树形图,那么我们可以计算
![g(z,\dots)=\prod_{k=1}^K[g_k(z,\dots)]](https://s0.wp.com/latex.php?latex=g%28z%2C%5Cdots%29%3D%5Cprod_%7Bk%3D1%7D%5EK%5Bg_k%28z%2C%5Cdots%29%5D&bg=f0f0f0&fg=555555&s=0&c=20201002)
其中,z出现在每个因式(factor) ,但是所有其他的变量(variables)只出现在一个因式中。
,但是所有其他的变量(variables)只出现在一个因式中。
例如,前面的一个例子,![f(x_1,\dots)=[f_1(x_1,x_2,x_3)][f_2(x_1,x_4,x_6)f_3(x_4)f_4(x_4,x_5)]](https://s0.wp.com/latex.php?latex=f%28x_1%2C%5Cdots%29%3D%5Bf_1%28x_1%2Cx_2%2Cx_3%29%5D%5Bf_2%28x_1%2Cx_4%2Cx_6%29f_3%28x_4%29f_4%28x_4%2Cx_5%29%5D&bg=f0f0f0&fg=555555&s=0&c=20201002)
所以,K=2。并且如下图所示:

下面,我们再来分析 ,由于树的结构(永远是variable node与factor node相连)我们可以观察出
,由于树的结构(永远是variable node与factor node相连)我们可以观察出
![g_k(z,\dots)=h(z,z_1,\dots,z_J)\prod_{j=1}^J[h_j(z_j,\dots)],](https://s0.wp.com/latex.php?latex=g_k%28z%2C%5Cdots%29%3Dh%28z%2Cz_1%2C%5Cdots%2Cz_J%29%5Cprod_%7Bj%3D1%7D%5EJ%5Bh_j%28z_j%2C%5Cdots%29%5D%2C&bg=f0f0f0&fg=555555&s=0&c=20201002)
其中,z只出现在核心函数(kernel) 中,每一个
中,每一个 最多只出现两次,可能在核心函数,或者其中一个因式(factor)
最多只出现两次,可能在核心函数,或者其中一个因式(factor) 中。
中。
我们前面的那个例子,![f_2(x_1,x_4,x_6)f_3(x_4)f_4(x_4,x_5)=f_2(x_1,x_4,x_6)[f_3(x_4)f_4(x_4,x_5)][1]](https://s0.wp.com/latex.php?latex=f_2%28x_1%2Cx_4%2Cx_6%29f_3%28x_4%29f_4%28x_4%2Cx_5%29%3Df_2%28x_1%2Cx_4%2Cx_6%29%5Bf_3%28x_4%29f_4%28x_4%2Cx_5%29%5D%5B1%5D&bg=f0f0f0&fg=555555&s=0&c=20201002) 。
。
1.3 Message-passing
其中, 是核心函数。如下图所示:
是核心函数。如下图所示:

因此,我们可以计算![\sum_{\sim z}g_k(z,\dots)=\sum_{\sim z}h(z,z_1,\dots,z_J)\prod_{j=1}^J[h_j(z_j,\dots)]=\sum_{\sim z}h(z,z_1,\dots,z_J)\prod_{j=1}^J[\sum_{\sim z_j}h_j(z_j,\dots)]](https://s0.wp.com/latex.php?latex=%5Csum_%7B%5Csim+z%7Dg_k%28z%2C%5Cdots%29%3D%5Csum_%7B%5Csim+z%7Dh%28z%2Cz_1%2C%5Cdots%2Cz_J%29%5Cprod_%7Bj%3D1%7D%5EJ%5Bh_j%28z_j%2C%5Cdots%29%5D%3D%5Csum_%7B%5Csim+z%7Dh%28z%2Cz_1%2C%5Cdots%2Cz_J%29%5Cprod_%7Bj%3D1%7D%5EJ%5B%5Csum_%7B%5Csim+z_j%7Dh_j%28z_j%2C%5Cdots%29%5D&bg=f0f0f0&fg=555555&s=0&c=20201002)
可以看到,我们可以计算marginal 通过kernel函数
通过kernel函数 和单个的marginals
和单个的marginals 的乘积。
的乘积。
注意,这时我们应该能发现,每个 的结构与我们要计算的
的结构与我们要计算的 是完全一样的。我们可以利用recursive进行求解,直到到达树的叶子(leaves)。
是完全一样的。我们可以利用recursive进行求解,直到到达树的叶子(leaves)。
初始化:如果是函数,那么就是函数本身。如果是variable node,就初始化为1。
我们还是通过前面那个例子,说明信息如何传递(message-passing):


在叶子(leaves)node, 初始化为1,
初始化为1, 初始化为$f_3$。在factor node,利用前面提到的“通过kernel函数
初始化为$f_3$。在factor node,利用前面提到的“通过kernel函数 和单个的marginals
和单个的marginals 的乘积”来计算,在variable node就进行乘法运算。我们总结一下Message-passing rules,如下图:
的乘积”来计算,在variable node就进行乘法运算。我们总结一下Message-passing rules,如下图:

最后一个是最后一步(final step)。我们标注 为信息(message)。
为信息(message)。
2. Decoding algorithm for BEC
我们之所以要先讨论BEC,是因为BEC信道是最为简单,易于分析。
我们发出的信号为{0,1},接受到的信号{0,e,1},e为erasure,概率为 。
。
因为BEC不会引入错误,所以对于variable node,如果incoming message全是erasure,那么outgoing message就是erasure。否则,incoming message 应该会统一是0或1。而对于check node,如果有一个incoming message是erasure,那么outgoing message就是erasure。否则,outgoing message为所有incoming message模2加的结果。
3. Decoding algorithm for BMC
BMC包括BSC和BSAWGN信道。Decoding algorithm会用到section1中提到的概念。对于BMC,信息就代表了概率或者置信度(belief),所以这个算法也叫做 belief propagation(BP) algorithm。
在BMC中,假设发出的信号{-1,1}。 分别代表了1和-1的置信度。初始化,
分别代表了1和-1的置信度。初始化, 。在degree为K+1的variable node中,message-passing 规则是
。在degree为K+1的variable node中,message-passing 规则是
 ,
,
我们引入比率(ratio)r, . 因此,
. 因此,
 ,
,
为了简化计算,我们定义 , 所以
, 所以 
下面我们考虑check node。 每一个check node都有一个kernel function, , 这是每个check node的constraint function。
, 这是每个check node的constraint function。
所以,对于degree 是 J+1的check node来说,





(因为  )
)



同时,
因此, 。
。
综上,在variable node的规则是,
在check node的规则是,
这就是Message-passing algorithm 的来历。
, E_b代表了energy/bit, N_o代表了noise power spectral density。因此 C=E_b*S,N=N_o*B。
,即0 dB。当C/B减小时(带宽增大),
的值会随着C/B的减小而减小,那么极限
。因此我们求到了shannon limit,即ln2,-1.6dB。这是在带宽趋于无穷大的情况下得到的。这当然是一个理论值,是无法做到的。
才能保证可靠的信道传输。




